Simuliamo il moto parabolico in Python e Spyder
Eccomi qui con un brevissimo tutorial su come possiamo utilizzare Spyder per fare delle semplici simulazioni di fisica meccanica.
Come primo esperimento ho scelto di lavorare sul moto parabolico, classico problema di fisica del liceo che voglio provare a risolvere e simulare in Python utilizzando il tool Spyder.
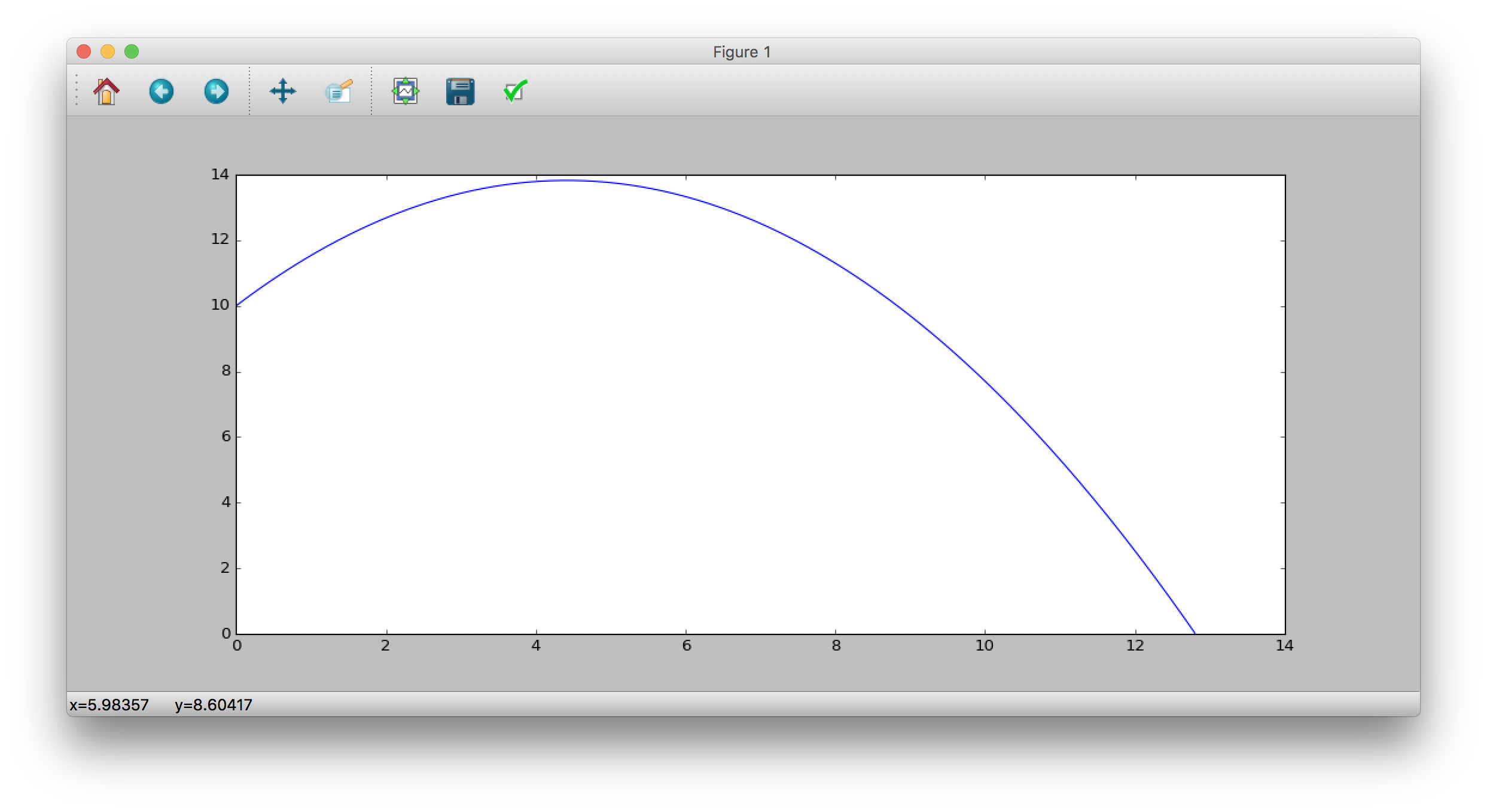
Scopo del tutorial
Quello che voglio fare, quindi, è scrivere un semplice e veloce programmino che permette di simulare il moto parabolico 2D, in particolare permettendo di
- calcolare gittata e tempo di volo;
- disegnare il grafico della traiettoria.
Un po' di teoria
Si definisce moto parabolico il moto bidimensionale di un corpo soggetto alla forza di gravità che percorre una traiettoria parabolica.
Se facciamo l'ipotesi che l'asse sia quello orizzontale e l'asse quello verticale e che l'accelerazione di gravità agisca verso il basso, quindi nel verso negativo rispetto all'asse
Il moto parabolico è la composizione bidimensionale di due moti distinti:
- Un moto lineare uniforme lungo l'asse orizzontale
- Un moto accelerato uniforme lungo l'asse verticale
In forma vettoriale, scriveremo
Dove è l'accelerazione di gravità, è l'altezza iniziale a cui viene lanciato il grave e e sono le componenti della velocità iniziale lungo i due assi e .
Solitamente si considera come istante di partenza e come posizione di partenza lungo l'asse .
Si noti che il moto parabolico termina quando si ha , si può quindi calcolare l'istante di tempo in cui il grave tocca terra ponendo
che si risolve, in , ottenendo
Una volta calcolato possiamo calcolare la posizione che corrisponde al punto sul terreno in cui il grave tocca terra:
Non mi voglio addentrare su considerazioni fisiche e meccaniche e su semplificazioni della formula trovata, che si possono fare in casi particolari per cui . Le soluzioni nella forma che abbiamo scritto fino ad ora bastano per poter risolvere il problema che ci siamo posti.
Simulazione in Python e Spyder
Una volta scaricato e installato Spyder ci troveremo davanti ad una finestra simile a questa.
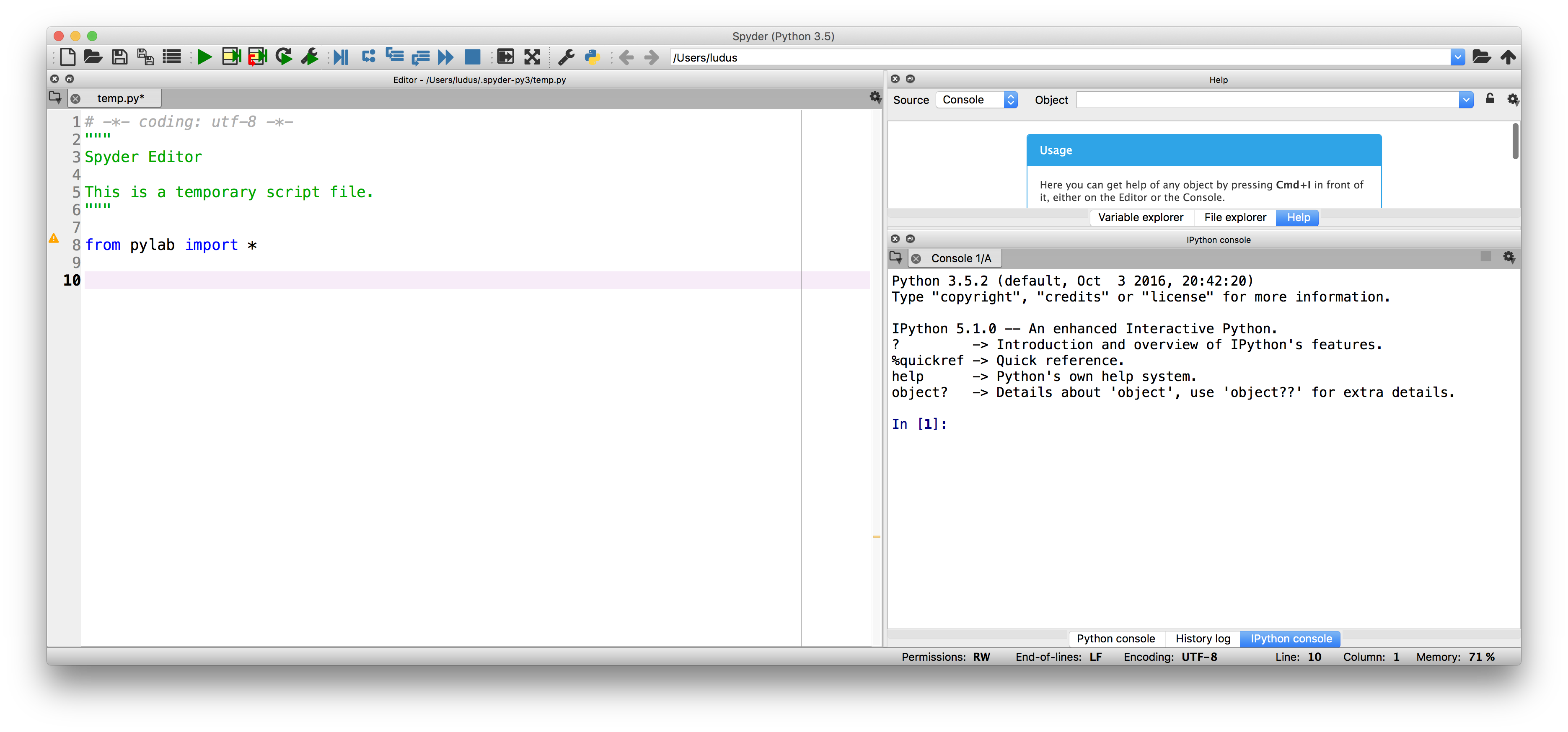
Nella finestra indicata come Editor (a me è mostrata sulla destra), possiamo andare ad implementare il codice che poi verrà eseguito da python. Sulla finistra indicata come Console potremo interagine utilizzando la console dinamica iPython. Per il momento, limitiamoci ad utilizzare l'editor di testo per rendere il programma più leggibile.
Importiamo pyLab
Per prima cosa, è importante importare tutti gli elementi di pyLab. pyLab è una suit python che include utilissimi moduli per l'analisi dei dati, come funzioni e costati matematiche (ad esempio sin o la costante indicata con pi) o la libreria per plottare plot.
from pylab import *
A questo punto, possiamo definire alcune variabili e costanti che useremo nel codice. Prima di tutto, è importante definire l'accelerazione di gravità
Definiamo variabili e costanti
g = 9.81 #m/s**2
e i valori numerici di velocità e altenzza iniziale.
v0 = 10. #m/s
alpha = pi/3 #radianti
h0 = 10. #m
Preferisco indicare la velocità iniziale utilizzando il suo modulo e l'angolo di inclinazione , da cui possiamo calcolare le componenti e che useremo nel codice
vx = v0*cos(alpha)
vy = v0*sin(alpha)
Calcoliamo tempo di volo e gittata
A questo punto, possiamo calcolare il tempo e la posizione finali del moto
tf = (vy + sqrt(vy**2+2*g*h0))/g
xf = vx*tf
Simulazione
A questo punto, possiamo scrivere il codice per la simulazione ed il disegno. Notiamo che non ha senso far prolungare la simulazione oltre il tempo . Per questo motivo, simuleremo solo nell'intervallo .
Per farlo, generiamo un array di campioni di tempo in questo intervallo ad un passo predefinito e piccolo, ad esempio con il comando arange
t = arange(0,tf, 0.01)
Adesso possiamo calcolare i valori di e per ogni tempo nell'array definito implementando semplicemente le equazioni del moto
xt = vx*t
yt = h0+vy*t-0.5*g*t**2
Si noti che Python sa che t e un array, e quindi genera come risultato degli array contenenti i valori delle equazioni ad ogni elemento di t. Comodo, no?
A questo punto, possiamo finalmente plottare (dall'inglese plot, cioè disegnare su un grafico) i due array.
plot(xt,yt)
Codice completo
Qui sotto trovate il codice completo appena implementato
# -*- coding: utf-8 -*-
"""
Spyder Editor
This is a temporary script file.
"""
from pylab import *
g = 9.81 #m/s**2
v0 = 10. #m/s
alpha = pi/3 #radianti
h0 = 10. #m
vx = v0*cos(alpha)
vy = v0*sin(alpha)
tf = (vy + sqrt(vy**2+2*g*h0))/g
xf = vx*tf
t = arange(0,tf, 0.01)
xt = vx*t
yt = h0+vy*t-0.5*g*t**2
plot(xt,yt)
Lanciamo il programma
Una volta implementato il codice, possiamo lanciare il programma premento sulla freccina verde in alto all'editor Spyder. Una volta fatto, se non ci sono errori, vedremo apparire il grafico della simulazione sulla console del nostro programma.
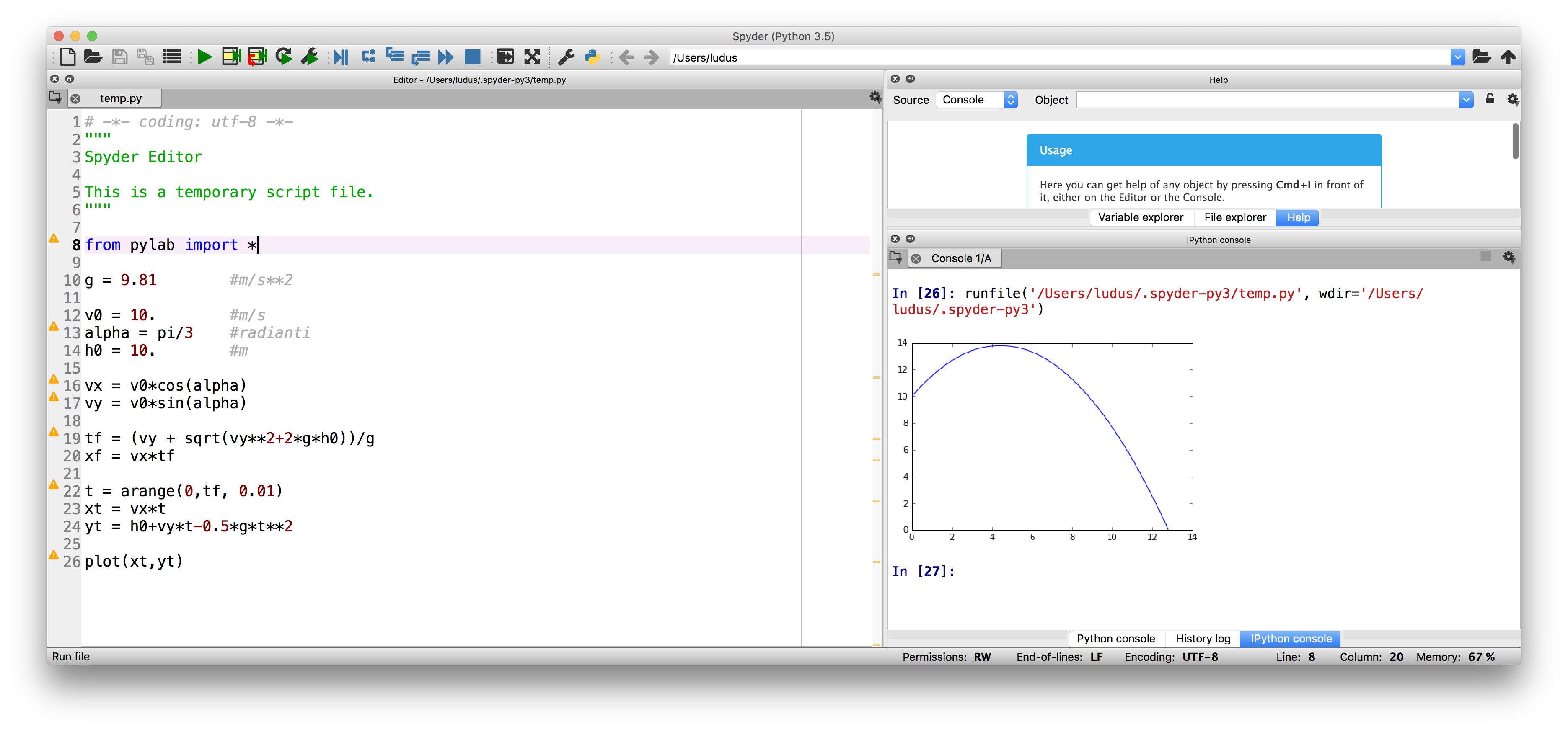
Conclusioni
Come vedete, in pochissime linee di codice siamo riusciti a risolvere in moto automatico un classico problema di fisica meccanica di base. Essendo tutto calcolato dal programma, possiamo anche fare esperimenti cambiando l'angolo e il modulo della velocità iniziale e/o l'altezza .
Buona sperimentazione a tutti!
Ringraziamenti
Alla stesura di questo documento hanno partecipato:
- Prof. Basilio Bona
